Die richtige Größe (Mensur) einer Gitarre bestimmen
Vor kurzem hatte ich einen jetzt Erstklässler vor mir sitzen, dem die Patentante die Gitarre schon besorgt hat. Der Erstklässler fällt als Kannkind eher klein aus und hatte eine ¾ Gitarre in der Hand. Ich würde zu einer halben Gitarre mit zierlichem Körper oder sogar zu einer ¼ Gitarre (48 cm) mit bulligen Körper neigen. Argument der Patentante: Wenn es eine kleine Gitarre wird, dann müsse man in einem halben Jahr eine neue Gitarre kaufen.
Ich war aus meinem Erfahrungshorizont erstaunt über diese Aussage. Aber ich war so perplex über diese Aussage, dass ich nicht darauf kam zu fragen, woran die Patentante, denn das festmachen würde.
Das Problem, die Patentante hat dasselbe studiert wie ich, hat dann aber Schulmusik drauf gesetzt und hat nach ein paar Jahren Unterrichten in den Schuldienst gewechselt.
Also wie begründe ich meine Einschätzungen, wie groß eine Gitarre sein muss? Ich gehe über die Dehnfähigkeit der Finger der linken Hand. (Konkret, ich lasse die Schüler*Innen an verschiedenen Stellen den ersten und dritten Finger gemeinsam aufsetzen, sodass ein Ganzton abgegriffen wird. Schaue mir die Spannung in der Hand an, indem ich die Finger dehne.) Ziel ist, dass diese Finger im Bereich ihrer aktiven Dehnfähigkeit bleiben können, sodass sie die an die linke Hand gestellten Aufgaben auch bewältigt werden können.
Wird dies nicht eingehalten, also die Mensur zu groß gewählt, dann
- ist nicht mehr möglich, dass derie SchülerIn die linke Hand ruhig lässt, weil die linke Hand nicht die nötige Dehnung zwischen den Fingern aufbringen kann.
- ist kein Legatospiel möglich, weil der Finger des ersten Tones schon vom Griffbrett abgehoben werden muss, um den nächsten zu greifen, weil die Finger die Dehnung nicht bewältigen können.
- ist kein Liegenlassen von Fingern und gemeinsames Greifen der Finger möglich. Frankfurt ist Teuchertland. Hier wird praktiziert, dass der tiefere Finger liegen bleibt, wenn ein höherer Finger auf derselben Saite folgt. Vice versa wird gemeinsam gegriffen. Das ist mit einer zu großen Mensur auch nicht möglich. Diese Vorgehensweise wird auch in anderen Methodiken praktiziert.
Ich habe von einem Kollegen eine Viertklässlerin übernommen. Er hat diese direkt nach der 52 cm Mensur auf eine 65 Mensur ohne Kapodaster geschickt. Sie musste plötzlich 1,4 cm mehr überbrücken. Ergebnis jeder Ton ist extrem kurz, weil die Finger vom Griffbrett gerissen werden müssen. Ich habe der SchülerIn wieder die 52-er Mensur verordnet und ihre Dehnfähigkeit getestet. Dritter Bund geht gerade so. Besser wäre vierter Bund. So weit hätte ich bisher gegenüber der Patentante argumentieren können.
Neuerdings kann ich viel mehr sagen. Die Schülerin hat momentan eine aktive Dehnfähigkeit von 45 – 48 mm. Nehme ich 48 mm an, dann wird dieses Kind als Erwachsene eine ¾ Gitarre spielen oder gerade so eine 7/8 Gitarre. Momentan müsste sie auf einer 65-er Mensur auf dem sechsten oder siebten Bund.spielen.
Für den Jungen mit der Patentante habe ich solch prognostische Tabelle aufgestellt.
| Alter | Körpergröße | Dehnung zwischen 1 und 3 | greift am 1. Bund | greift am 2. Bund | greift am 3. Bund | greift am 4. Bund | greift am 5. Bund | greift am 6. Bund |
|---|---|---|---|---|---|---|---|---|
| 6 Jahre | 117,8 cm | 4,5 cm | 43,5 cm | 46,0 cm | 48,8 cm | 51,7 cm | 54,7 cm | 58,0 cm |
| 6,5 Jahre | 121,1 cm | 4,6 cm | 44,7 cm | 47,3 cm | 50,2 cm | 53,1 cm | 56,3 cm | 59,6 cm |
| 7 Jahre | 124,5 cm | 4,7 cm | 45,9 cm | 48,7 cm | 51,6 cm | 54,6 cm | 57,9 cm | 61,3 cm |
| 7,5 Jahre | 127,8 cm | 4,9 cm | 47,1 cm | 49,9 cm | 52,9 cm | 56,1 cm | 59,4 cm | 62,9 cm |
| 8 Jahre | 130,8 cm | 5,0 cm | 48,3 cm | 51,1 cm | 54,2 cm | 57,4 cm | 60,8 cm | 64,4 cm |
| 8,5 Jahre | 133,6 cm | 5,1 cm | 49,3 cm | 52,2 cm | 55,3 cm | 58,6 cm | 62,1 cm | 65,8 cm |
| 9 Jahre | 136,4 cm | 5,2 cm | 50,3 cm | 53,3 cm | 56,5 cm | 59,8 cm | 63,4 cm | 67,1 cm |
| 9,5 Jahre | 139,0 cm | 5,3 cm | 51,3 cm | 54,3 cm | 57,6 cm | 61,0 cm | 64,6 cm | 68,4 cm |
| 10 Jahre | 141,6 cm | 5,4 cm | 52,2 cm | 55,3 cm | 58,6 cm | 62,1 cm | 65,8 cm | 69,7 cm |
| 10,5 Jahre | 144,1 cm | 5,5 cm | 53,2 cm | 56,3 cm | 59,7 cm | 63,2 cm | 67,0 cm | 71,0 cm |
| 11 Jahre | 146,7 cm | 5,6 cm | 54,1 cm | 57,3 cm | 60,7 cm | 64,4 cm | 68,2 cm | 72,2 cm |
| 11,5 Jahre | 149,4 cm | 5,7 cm | 55,1 cm | 58,4 cm | 61,8 cm | 65,5 cm | 69,4 cm | 73,5 cm |
| 12 Jahre | 152,2 cm | 5,8 cm | 56,2 cm | 59,5 cm | 63,0 cm | 66,8 cm | 70,8 cm | 75,0 cm |
| 12,5 Jahre | 155,4 cm | 5,9 cm | 57,3 cm | 60,8 cm | 64,4 cm | 68,2 cm | 72,2 cm | 76,5 cm |
| 13 Jahre | 159,1 cm | 6,0 cm | 58,7 cm | 62,2 cm | 65,9 cm | 69,8 cm | 74,0 cm | 78,4 cm |
| 13,5 Jahre | 163,1 cm | 6,2 cm | 60,2 cm | 63,7 cm | 67,5 cm | 71,6 cm | 75,8 cm | 80,3 cm |
| 14 Jahre | 166,9 cm | 6,3 cm | 61,6 cm | 65,2 cm | 69,1 cm | 73,2 cm | 77,6 cm | 82,2 cm |
| 14,5 Jahre | 170,4 cm | 6,5 cm | 62,8 cm | 66,6 cm | 70,5 cm | 74,7 cm | 79,2 cm | 83,9 cm |
| 15 Jahre | 173,1 cm | 6,6 cm | 63,9 cm | 67,7 cm | 71,7 cm | 76,0 cm | 80,5 cm | 85,3 cm |
| 15,5 Jahre | 175,2 cm | 6,7 cm | 64,6 cm | 68,5 cm | 72,5 cm | 76,9 cm | 81,4 cm | 86,3 cm |
| 16 Jahre | 176,7 cm | 6,7 cm | 65,2 cm | 69,0 cm | 73,2 cm | 77,5 cm | 82,1 cm | 87,0 cm |
| 16,5 Jahre | 177,6 cm | 6,7 cm | 65,5 cm | 69,4 cm | 73,6 cm | 77,9 cm | 82,6 cm | 87,5 cm |
| 17 Jahre | 178,2 cm | 6,8 cm | 65,8 cm | 69,7 cm | 73,8 cm | 78,2 cm | 82,8 cm | 87,8 cm |
| 17,5 Jahre | 178,7 cm | 6,8 cm | 65,9 cm | 69,8 cm | 74,0 cm | 78,4 cm | 83,1 cm | 88,0 cm |
| 18 Jahre | 179,0 cm | 6,8 cm | 66,1 cm | 70,0 cm | 74,1 cm | 78,5 cm | 83,2 cm | 88,2 cm |
Woher der neue Wissensstand? Ich hatte das Problem, wie argumentiere ich notfalls gegen die Patentante. Das Argument ich probiere das aus und 30 Jahre Erfahrung gegen ein paar Jahre ist dann plötzlich ein sehr dünner Argumentationsboden.
Also wollte ich meine Einschätzung objektivieren. Dass die Tabellen, die die Gitarrengröße vom Alter abhängig machen, mir Recht geben, war mir zu wenig, weil ich die Idee die Größe über das Alter zu bestimmen für fragwürdig halte. Das relevante Maß ist die linke Hand. Es gibt kleine Hände zu großen Körper. Es gibt dehnfähige Hände, es gibt Hände, die bekommen die Finger nicht auseinander. Wenn die Finger in die Spielhaltung gehen, laufen die Finger zusammen. Je nach Winkel, wie die Finger zusammenlaufen, sind die Fingerkuppen unterschiedlich stark entfernt. Bei so vielen Faktoren, das Alter als Maßstab nehmen, fand ich fragwürdig.
Deswegen schaute ich bei der EGTA nach und fand dieses PDF. Körpergröße mal 0,36. Leider wird nicht offen gelegt, warum man auf den Faktor 0,36 kommt. Auch verwunderte mich, dass keine geschlechtsspezifische Spanne des Faktors angegeben wird.
Frauen sollen tendenziell kleinere Hände im Verhältnis zur Körpergröße haben als Männer. Ich habe einen Schüler der mit 67 angefangen hat und ca. 1,90 groß ist. Nach Formel könnte er 68,4 cm spielen. In Realität dürften wegen des altersbedingten Verlustes der Dehnfähigkeit 63 cm schon an seiner Schmerzgrenze sein.
Für mich kommen 2 Zentimeter zu viel raus. Unter „objektiv feststellbar“ verstehe ich etwas anderes.
Ich kam plötzlich auf die Idee, ich könnte die Spanne zwischen meinem erstem und drittem Finger ausmessen und diesen in die nötige Mensur umzurechnen. Ich griff in meiner Werkzeugschublade zu meinem Zollstock und sah meinen Me ss schieber daneben. Messschieber schien mir intuitiv ein genaueres Ergebnis zu erzeugen. Ich probierte herum und auch an meinen SchülerInnen und merkte, die Messschiebermessung hat eine zu hohe Schwankung bei Messwiederholungen.
Es stellten sich weitere, nicht zu beantwortende Fragen heraus.
- Verhalten sich die Finger wirklich so wie an einem Gitarrenhals?
- Wenn ich die Spanne zwischen erstem und drittem Finger messe,
- muss ich die Breite des ersten Fingers abziehen oder nur einen Teil der Breite des ersten Fingers. Oder muss auch eine Teilbreite des dritten Fingers abgezogen werden. Wenn ja, wie bestimmt man die Breite. (Zur Erklärung. Es gibt Menschen, da ragt die Innenseite des ersten Fingers gut erkennbar in den nächsten Bund.)
- Wo und wie setzt man den Messschieber am besten an.
- Ich persönlich teste bei meiner bisherigen Methode unter anderem den Widerstand der passiven Dehnung, wenn erster und dritter Finger greifen. Ist mir der Widerstand zu hoch, rücke ich einen Bund höher. Diesen Widerstand bei dieser Messmethode zu „messen“ ist manuell nicht möglich. Oder ich war zu phantasielos.
Dann fiel es mir wie Schuppen vor die Augen. Man kann die SchülerInnenfinger auf dem Griffbrett einer Gitarre hin und herschieben, bis man eine Position gefunden hat, die gut aussieht, bzw. ich beim Test der passiven Dehnfähigkeit, nicht das Gefühl habe, im sicheren Abstand zur Schmerzgrenze zu sein. Nehme den Abstand zwischen den Bünden und berechnet damit die nötige Mensur.
Hier ein Tabelle der Bundabstände der mir bekannten auf dem Markt erhältlichen Mensuren, wenn man einen Ganzton auf einer Saite greift.
| Mensur der Gitarre | 1. Bund | 2. Bund | 3. Bund | 4. Bund | 5. Bund |
|---|---|---|---|---|---|
| 65 cm | 6,7 cm | 6,3 cm | 6,0 cm | 5,6 cm | 5,3 cm |
| 63 cm | 6,5 cm | 6,1 cm | 5,8 cm | 5,5 cm | 5,1 cm |
| 62 cm | 6,4 cm | 6,0 cm | 5,7 cm | 5,4 cm | 5,1 cm |
| 59 cm | 6,1 cm | 5,7 cm | 5,4 cm | 5,1 cm | 4,8 cm |
| 58 cm | 6,0 cm | 5,6 cm | 5,3 cm | 5,0 cm | 4,7 cm |
| 57 cm | 5,9 cm | 5,5 cm | 5,2 cm | 4,9 cm | 4,7 cm |
| 53 cm | 5,5 cm | 5,2 cm | 4,9 cm | 4,6 cm | 4,3 cm |
| 52 cm | 5,4 cm | 5,1 cm | 4,8 cm | 4,5 cm | 4,3 cm |
| 48 cm | 4,9 cm | 4,7 cm | 4,4 cm | 4,2 cm | 3,9 cm |
| 47 cm | 4,8 cm | 4,6 cm | 4,3 cm | 4,1 cm | 3,8 cm |
| 44 cm | 4,5 cm | 4,3 cm | 4,0 cm | 3,8 cm | 3,6 cm |
| 41 cm | 4,2 cm | 4,0 cm | 3,8 cm | 3,6 cm | 3,4 cm |
Jedem*r wird auffallen, dass wenn man die Differenz zwischen den Abständen anzieht, dass sich diese Differenz zwischen 3 – 4, 5 Millimeter handelt. Das ist doch wenig, kann man das nicht ausgleichen, wenn man sich ein wenig anstrengt. Sind diese Differenzen jetzt ein Klacks für die Kinderhand. (Wenn man meine obige vorweggenommene Tabelle ansieht, stellt man fest, es handelt sich um knapp zwei Jahre Wachstum.)
Deswegen stellte ich mir die Frage, gibt es Statistiken, wie Hände wachsen. Ich habe keine gefunden, aber eine Statistik über das Körperwachstum zwischen dem zweiten und zwanzigsten Lebensjahr. https://www.cdc.gov/growthcharts/html_charts/statage.htm#males und https://www.cdc.gov/growthcharts/html_charts/statage.htm#females
Solche Statistiken sollte man als Instrumentallehrer kennen.
Erst einmal, mir und allen anderen Lehrkräften von mitwachsenden Instrumenten wird die Frage gestellt, wann und wie oft müssen wir ein neues Instrument kaufen. Eine Frage, die ich und wahrscheinlich alle anderen ungern beantworten, weil Wachstum bei Kindern ist ja so unvorhersehbar. So ebenfalls eine weit verbreitete Ansicht. Sieht man sich diese Statistiken an, stellt man fest, dass Kinder pro Jahr einen gewissen Betrag wachsen, der kontinuierlich abnimmt. Ich habe die Wachstumkurven der KIGGS-Studie visualisiert. Diese Studie ist eine beinhaltet die Größen deutscher Kinder.
Ich habe die Wachstumsverläufe der einzelnen Kohorten visualisiert.
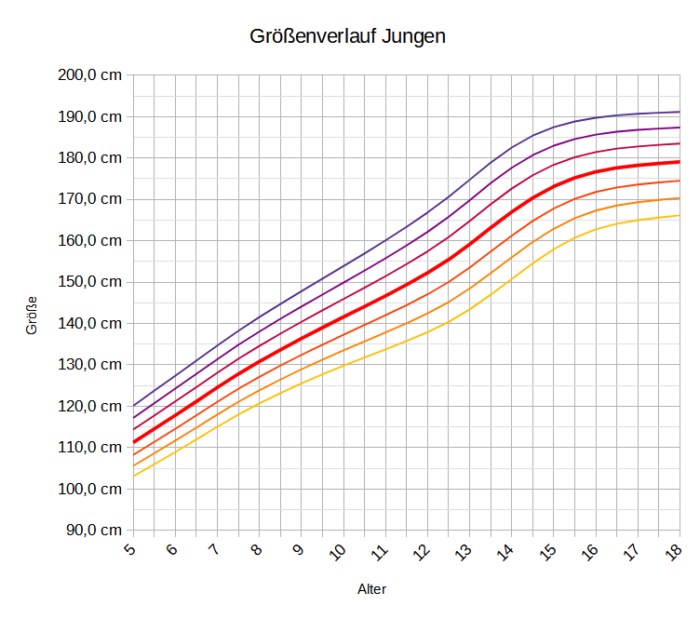
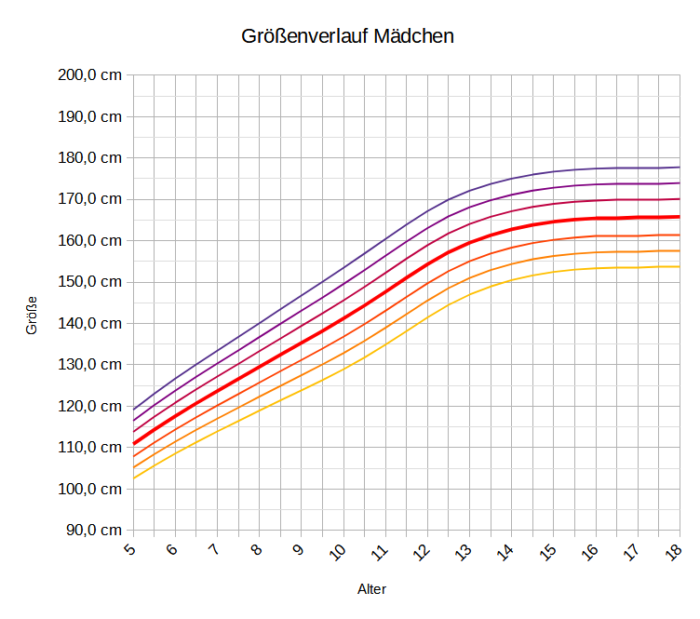
Von dem regelmäßigen Verlauf dieser Wachstumskurven beeindruckt, habe ich die Wachstumsintervalle für die Altersstufen berechnet. Einerseits graphisch dargestellt.

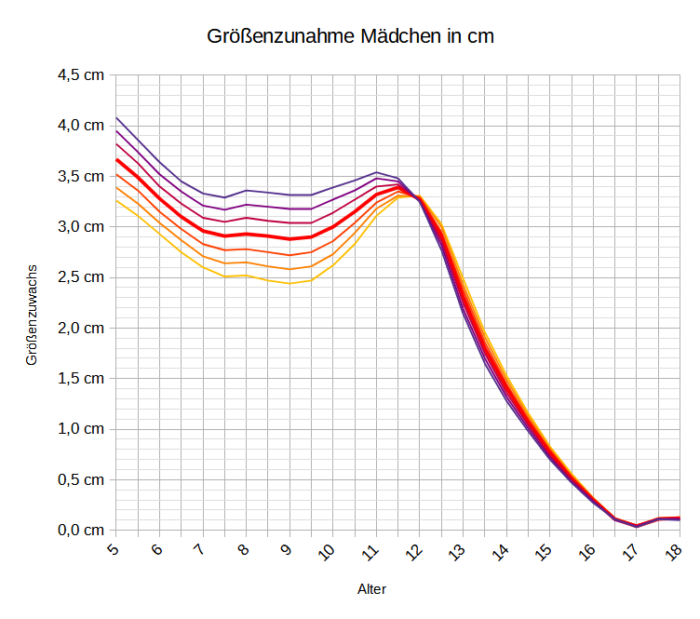
Und hier in einer Tabelle
Zuwächse Jungen in cm
| Alter/Anfangsgröße | 103,0 cm | 105,6 cm | 108,2 cm | 111,2 cm | 114,3 cm | 117,2 cm | 120,1 cm |
|---|---|---|---|---|---|---|---|
| 5 | 2,9 cm | 3,0 cm | 3,2 cm | 3,3 cm | 3,4 cm | 3,6 cm | 3,7 cm |
| 5.5 | 2,9 cm | 3,0 cm | 3,2 cm | 3,3 cm | 3,4 cm | 3,5 cm | 3,7 cm |
| 6 | 2,9 cm | 3,0 cm | 3,1 cm | 3,3 cm | 3,4 cm | 3,5 cm | 3,6 cm |
| 6.5 | 3,1 cm | 3,2 cm | 3,2 cm | 3,3 cm | 3,5 cm | 3,6 cm | 3,6 cm |
| 7 | 3,1 cm | 3,2 cm | 3,3 cm | 3,4 cm | 3,5 cm | 3,6 cm | 3,6 cm |
| 7.5 | 3,0 cm | 3,1 cm | 3,2 cm | 3,3 cm | 3,4 cm | 3,5 cm | 3,6 cm |
| 8 | 2,7 cm | 2,8 cm | 2,9 cm | 3,0 cm | 3,1 cm | 3,2 cm | 3,3 cm |
| 8.5 | 2,5 cm | 2,6 cm | 2,7 cm | 2,8 cm | 3,0 cm | 3,1 cm | 3,2 cm |
| 9 | 2,3 cm | 2,5 cm | 2,6 cm | 2,7 cm | 2,9 cm | 3,0 cm | 3,1 cm |
| 9.5 | 2,2 cm | 2,3 cm | 2,5 cm | 2,6 cm | 2,8 cm | 2,9 cm | 3,0 cm |
| 10 | 2,1 cm | 2,2 cm | 2,4 cm | 2,6 cm | 2,8 cm | 2,9 cm | 3,0 cm |
| 10.5 | 2,0 cm | 2,2 cm | 2,3 cm | 2,5 cm | 2,7 cm | 2,9 cm | 3,0 cm |
| 11 | 2,0 cm | 2,2 cm | 2,4 cm | 2,6 cm | 2,8 cm | 3,0 cm | 3,2 cm |
| 11.5 | 2,0 cm | 2,2 cm | 2,4 cm | 2,7 cm | 2,9 cm | 3,1 cm | 3,3 cm |
| 12 | 2,2 cm | 2,4 cm | 2,6 cm | 2,9 cm | 3,1 cm | 3,3 cm | 3,5 cm |
| 12.5 | 2,5 cm | 2,7 cm | 3,0 cm | 3,2 cm | 3,4 cm | 3,6 cm | 3,8 cm |
| 13 | 3,0 cm | 3,3 cm | 3,5 cm | 3,7 cm | 3,9 cm | 4,0 cm | 4,1 cm |
| 13.5 | 3,5 cm | 3,7 cm | 3,8 cm | 4,0 cm | 4,1 cm | 4,1 cm | 4,2 cm |
| 14 | 3,8 cm | 3,8 cm | 3,8 cm | 3,8 cm | 3,8 cm | 3,7 cm | 3,6 cm |
| 14.5 | 3,8 cm | 3,7 cm | 3,6 cm | 3,4 cm | 3,2 cm | 3,1 cm | 2,9 cm |
| 15 | 3,4 cm | 3,2 cm | 3,0 cm | 2,8 cm | 2,5 cm | 2,3 cm | 2,0 cm |
| 15.5 | 2,8 cm | 2,6 cm | 2,3 cm | 2,1 cm | 1,8 cm | 1,6 cm | 1,4 cm |
| 16 | 2,0 cm | 1,8 cm | 1,7 cm | 1,5 cm | 1,3 cm | 1,1 cm | 0,9 cm |
| 16.5 | 1,3 cm | 1,2 cm | 1,1 cm | 1,0 cm | 0,8 cm | 0,7 cm | 0,6 cm |
| 17 | 0,9 cm | 0,8 cm | 0,7 cm | 0,6 cm | 0,5 cm | 0,4 cm | 0,4 cm |
| 17.5 | 0,6 cm | 0,6 cm | 0,5 cm | 0,4 cm | 0,4 cm | 0,3 cm | 0,3 cm |
| 18 | 0,5 cm | 0,5 cm | 0,4 cm | 0,4 cm | 0,3 cm | 0,3 cm | 0,2 cm |
| Endgröße | 166,1 cm | 170,3 cm | 174,5 cm | 179,0 cm | 183,5 cm | 187,4 cm | 191,1 cm |
Zuwächse Mädchen in cm
| Alter/Anfangsgröße | 105,6 cm | 108,4 cm | 111,2 cm | 114,3 cm | 117,4 cm | 120,2 cm | 123,0 cm |
|---|---|---|---|---|---|---|---|
| 5 | 3,3 cm | 3,4 cm | 3,5 cm | 3,7 cm | 3,8 cm | 3,9 cm | 4,1 cm |
| 5.5 | 3,1 cm | 3,2 cm | 3,4 cm | 3,5 cm | 3,6 cm | 3,7 cm | 3,9 cm |
| 6 | 2,9 cm | 3,0 cm | 3,2 cm | 3,3 cm | 3,4 cm | 3,5 cm | 3,6 cm |
| 6.5 | 2,8 cm | 2,9 cm | 3,0 cm | 3,1 cm | 3,2 cm | 3,3 cm | 3,5 cm |
| 7 | 2,6 cm | 2,7 cm | 2,8 cm | 3,0 cm | 3,1 cm | 3,2 cm | 3,3 cm |
| 7.5 | 2,5 cm | 2,6 cm | 2,8 cm | 2,9 cm | 3,0 cm | 3,2 cm | 3,3 cm |
| 8 | 2,5 cm | 2,7 cm | 2,8 cm | 2,9 cm | 3,1 cm | 3,2 cm | 3,4 cm |
| 8.5 | 2,5 cm | 2,6 cm | 2,7 cm | 2,9 cm | 3,1 cm | 3,2 cm | 3,3 cm |
| 9 | 2,4 cm | 2,6 cm | 2,7 cm | 2,9 cm | 3,0 cm | 3,2 cm | 3,3 cm |
| 9.5 | 2,5 cm | 2,6 cm | 2,8 cm | 2,9 cm | 3,0 cm | 3,2 cm | 3,3 cm |
| 10 | 2,6 cm | 2,7 cm | 2,9 cm | 3,0 cm | 3,1 cm | 3,3 cm | 3,4 cm |
| 10.5 | 2,8 cm | 2,9 cm | 3,0 cm | 3,2 cm | 3,3 cm | 3,4 cm | 3,5 cm |
| 11 | 3,1 cm | 3,2 cm | 3,2 cm | 3,3 cm | 3,4 cm | 3,5 cm | 3,5 cm |
| 11.5 | 3,3 cm | 3,3 cm | 3,3 cm | 3,4 cm | 3,4 cm | 3,4 cm | 3,5 cm |
| 12 | 3,3 cm | 3,3 cm | 3,3 cm | 3,3 cm | 3,3 cm | 3,3 cm | 3,3 cm |
| 12.5 | 3,0 cm | 3,0 cm | 3,0 cm | 2,9 cm | 2,9 cm | 2,8 cm | 2,8 cm |
| 13 | 2,5 cm | 2,4 cm | 2,4 cm | 2,3 cm | 2,3 cm | 2,2 cm | 2,1 cm |
| 13.5 | 2,0 cm | 1,9 cm | 1,9 cm | 1,8 cm | 1,8 cm | 1,7 cm | 1,6 cm |
| 14 | 1,5 cm | 1,5 cm | 1,5 cm | 1,4 cm | 1,4 cm | 1,3 cm | 1,3 cm |
| 14.5 | 1,2 cm | 1,1 cm | 1,1 cm | 1,1 cm | 1,0 cm | 1,0 cm | 1,0 cm |
| 15 | 0,8 cm | 0,8 cm | 0,8 cm | 0,8 cm | 0,7 cm | 0,7 cm | 0,7 cm |
| 15.5 | 0,6 cm | 0,5 cm | 0,5 cm | 0,5 cm | 0,5 cm | 0,5 cm | 0,5 cm |
| 16 | 0,3 cm | 0,3 cm | 0,3 cm | 0,3 cm | 0,3 cm | 0,3 cm | 0,3 cm |
| 16.5 | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm |
| 17 | 0,0 cm | 0,0 cm | 0,0 cm | 0,0 cm | 0,0 cm | 0,0 cm | 0,0 cm |
| 17.5 | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm |
| 18 | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm | 0,1 cm |
| Endgröße | 153,8 cm | 157,6 cm | 161,5 cm | 165,8 cm | 170,1 cm | 174,0 cm | 177,8 cm |
Es ist zu erkennen, Kinder wachsen nicht so sprunghaft, wie man gemeinhin annimmt, sondern sie wachsen um einen ähnlichen Betrag wie im vorigen Zeitraum.
Plötzlich kam mir die Idee, drücke doch diese Unterschiede in Prozenten aus. Dann sieht man etwas, was man vermutlich nicht geglaubt hat. Kinder einer Altersstufe wachsen in einem bestimmten Zeitabschnitt prozentual nahezu um den gleichen Betrag.
Zuerst die Grafiken.
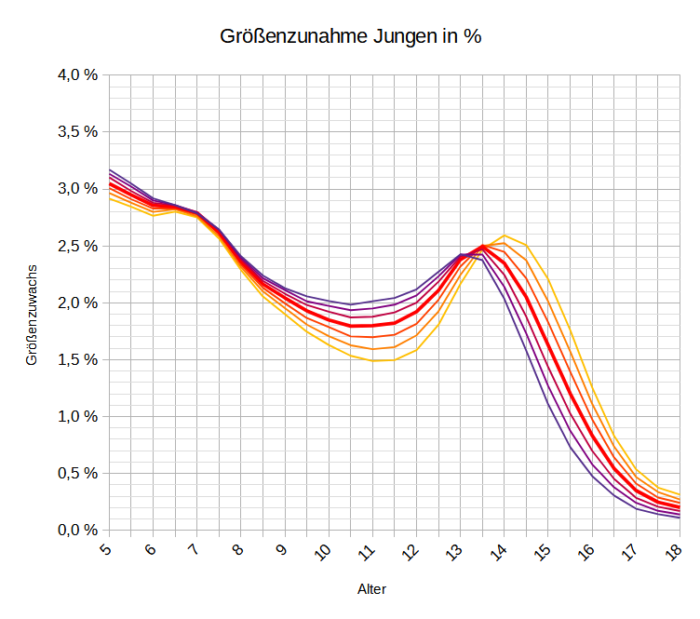
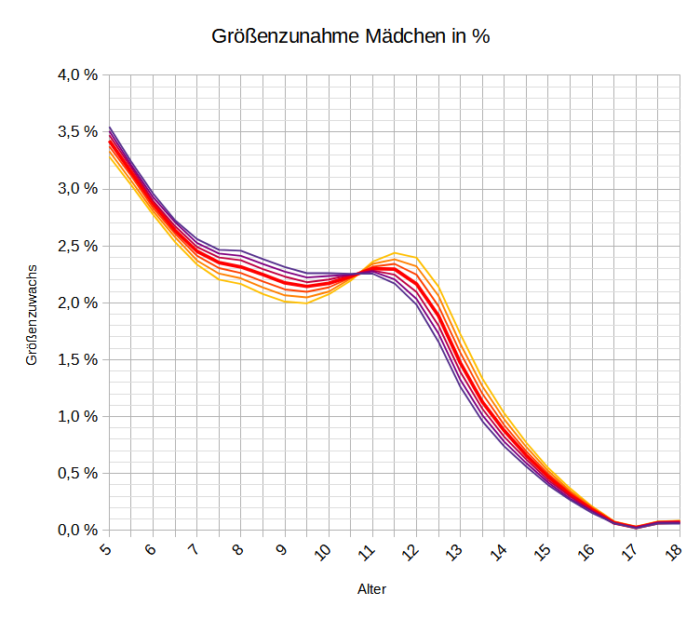
Und als Tabelle.
Zuwächse Jungen in Prozent
| Alter/Anfangsgröße | 103,0 cm | 105,6 cm | 108,2 cm | 111,2 cm | 114,3 cm | 117,2 cm | 120,1 cm |
|---|---|---|---|---|---|---|---|
| 5 | 2,9 % | 3,0 % | 3,0 % | 3,0 % | 3,1 % | 3,1 % | 3,2 % |
| 5,5 | 2,8 % | 2,9 % | 2,9 % | 2,9 % | 3,0 % | 3,0 % | 3,0 % |
| 6 | 2,8 % | 2,8 % | 2,8 % | 2,9 % | 2,9 % | 2,9 % | 2,9 % |
| 6,5 | 2,8 % | 2,8 % | 2,8 % | 2,8 % | 2,9 % | 2,9 % | 2,9 % |
| 7 | 2,8 % | 2,8 % | 2,8 % | 2,8 % | 2,8 % | 2,8 % | 2,8 % |
| 7,5 | 2,6 % | 2,6 % | 2,6 % | 2,6 % | 2,6 % | 2,6 % | 2,6 % |
| 8 | 2,3 % | 2,3 % | 2,3 % | 2,4 % | 2,4 % | 2,4 % | 2,4 % |
| 8,5 | 2,1 % | 2,1 % | 2,1 % | 2,2 % | 2,2 % | 2,2 % | 2,2 % |
| 9 | 1,9 % | 2,0 % | 2,0 % | 2,0 % | 2,1 % | 2,1 % | 2,1 % |
| 9,5 | 1,7 % | 1,8 % | 1,9 % | 1,9 % | 2,0 % | 2,0 % | 2,1 % |
| 10 | 1,6 % | 1,7 % | 1,8 % | 1,8 % | 1,9 % | 2,0 % | 2,0 % |
| 10,5 | 1,5 % | 1,6 % | 1,7 % | 1,8 % | 1,9 % | 1,9 % | 2,0 % |
| 11 | 1,5 % | 1,6 % | 1,7 % | 1,8 % | 1,9 % | 2,0 % | 2,0 % |
| 11,5 | 1,5 % | 1,6 % | 1,7 % | 1,8 % | 1,9 % | 2,0 % | 2,0 % |
| 12 | 1,6 % | 1,7 % | 1,8 % | 1,9 % | 2,0 % | 2,1 % | 2,1 % |
| 12,5 | 1,8 % | 1,9 % | 2,0 % | 2,1 % | 2,2 % | 2,2 % | 2,3 % |
| 13 | 2,2 % | 2,2 % | 2,3 % | 2,4 % | 2,4 % | 2,4 % | 2,4 % |
| 13,5 | 2,5 % | 2,5 % | 2,5 % | 2,5 % | 2,5 % | 2,4 % | 2,4 % |
| 14 | 2,6 % | 2,5 % | 2,4 % | 2,3 % | 2,2 % | 2,1 % | 2,0 % |
| 14,5 | 2,5 % | 2,4 % | 2,2 % | 2,0 % | 1,9 % | 1,7 % | 1,6 % |
| 15 | 2,2 % | 2,0 % | 1,8 % | 1,6 % | 1,4 % | 1,3 % | 1,1 % |
| 15,5 | 1,8 % | 1,6 % | 1,4 % | 1,2 % | 1,0 % | 0,9 % | 0,7 % |
| 16 | 1,3 % | 1,1 % | 1,0 % | 0,8 % | 0,7 % | 0,6 % | 0,5 % |
| 16,5 | 0,8 % | 0,7 % | 0,6 % | 0,5 % | 0,5 % | 0,4 % | 0,3 % |
| 17 | 0,5 % | 0,5 % | 0,4 % | 0,3 % | 0,3 % | 0,2 % | 0,2 % |
| 17,5 | 0,4 % | 0,3 % | 0,3 % | 0,2 % | 0,2 % | 0,2 % | 0,1 % |
| 18 | 0,3 % | 0,3 % | 0,2 % | 0,2 % | 0,2 % | 0,1 % | 0,1 % |
| Endgröße | 166,1 cm | 170,3 cm | 174,5 cm | 179,0 cm | 183,5 cm | 187,4 cm | 191,1 cm |
Zuwächse Mädchen in Prozent
| Alter/Anfangsgröße | 105,6 cm | 108,4 cm | 111,2 cm | 114,3 cm | 117,4 cm | 120,2 cm | 123,0 cm |
|---|---|---|---|---|---|---|---|
| 5 | 3,30 % | 3,30 % | 3,40 % | 3,40 % | 3,50 % | 3,50 % | 3,50 % |
| 5,5 | 3,00 % | 3,10 % | 3,10 % | 3,10 % | 3,20 % | 3,20 % | 3,20 % |
| 6 | 2,80 % | 2,80 % | 2,80 % | 2,90 % | 2,90 % | 2,90 % | 3,00 % |
| 6,5 | 2,50 % | 2,60 % | 2,60 % | 2,60 % | 2,70 % | 2,70 % | 2,70 % |
| 7 | 2,30 % | 2,40 % | 2,40 % | 2,50 % | 2,50 % | 2,50 % | 2,60 % |
| 7,5 | 2,20 % | 2,30 % | 2,30 % | 2,40 % | 2,40 % | 2,40 % | 2,50 % |
| 8 | 2,20 % | 2,20 % | 2,30 % | 2,30 % | 2,40 % | 2,40 % | 2,50 % |
| 8,5 | 2,10 % | 2,10 % | 2,20 % | 2,20 % | 2,30 % | 2,30 % | 2,40 % |
| 9 | 2,00 % | 2,10 % | 2,10 % | 2,20 % | 2,20 % | 2,30 % | 2,30 % |
| 9,5 | 2,00 % | 2,00 % | 2,10 % | 2,10 % | 2,20 % | 2,20 % | 2,30 % |
| 10 | 2,10 % | 2,10 % | 2,10 % | 2,20 % | 2,20 % | 2,20 % | 2,30 % |
| 10,5 | 2,20 % | 2,20 % | 2,20 % | 2,20 % | 2,20 % | 2,20 % | 2,30 % |
| 11 | 2,40 % | 2,30 % | 2,30 % | 2,30 % | 2,30 % | 2,30 % | 2,30 % |
| 11,5 | 2,40 % | 2,40 % | 2,30 % | 2,30 % | 2,20 % | 2,20 % | 2,20 % |
| 12 | 2,40 % | 2,30 % | 2,20 % | 2,20 % | 2,10 % | 2,00 % | 2,00 % |
| 12,5 | 2,10 % | 2,10 % | 2,00 % | 1,90 % | 1,80 % | 1,70 % | 1,70 % |
| 13 | 1,70 % | 1,60 % | 1,60 % | 1,50 % | 1,40 % | 1,30 % | 1,30 % |
| 13,5 | 1,30 % | 1,30 % | 1,20 % | 1,10 % | 1,10 % | 1,00 % | 1,00 % |
| 14 | 1,00 % | 1,00 % | 0,90 % | 0,90 % | 0,80 % | 0,80 % | 0,70 % |
| 14,5 | 0,80 % | 0,70 % | 0,70 % | 0,70 % | 0,60 % | 0,60 % | 0,60 % |
| 15 | 0,50 % | 0,50 % | 0,50 % | 0,50 % | 0,40 % | 0,40 % | 0,40 % |
| 15,5 | 0,40 % | 0,30 % | 0,30 % | 0,30 % | 0,30 % | 0,30 % | 0,30 % |
| 16 | 0,20 % | 0,20 % | 0,20 % | 0,20 % | 0,20 % | 0,20 % | 0,20 % |
| 16,5 | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % |
| 17 | 0,00 % | 0,00 % | 0,00 % | 0,00 % | 0,00 % | 0,00 % | 0,00 % |
| 17,5 | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % |
| 18 | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % | 0,10 % |
| Endgröße | 153,8 cm | 157,6 cm | 161,5 cm | 165,8 cm | 170,1 cm | 174,0 cm | 177,8 cm |
Ob dieser Regelmäßigkeiten gehe ich davon aus, dass es solche Kurven für das Wachstum von Händen gibt, sofern sich jemand die Mühe gemacht hat, solche Kurven zu erstellen. Diese Kurven würden damit für das Wachstum der Dehnung zwischen den Fingern gelten.
Am schönsten wäre, das Verhältnis Hand Körper bleibt in der Wachstumsphase konstant.
Die Frage ist, bleibt das Verhältnis Handgröße und Körpergröße gleich oder ändert es sich? Danach habe ich gesucht und eine halb(un)befriedigende Antwort gefunden.
Es gibt Studien, die feststellen, man könne, anhand der Handgröße, die Körpergröße bestimmen. Sie geben auch eine geschlechtsspezifischen Faktor für das Verhältnis Körper und Hand an. Aber es wurden nur erwachsene Menschen untersucht. Eine der Formeln lautet:
Körperhöhe = 80,400 + 5,122 * Handgröße – 0,195 * Alter + 6,383 * (Geschlecht: Frau = 0, Mann =1)
Jeder*m, die Ahnung von Mathematik hat, fällt auf, dass das keine direkte Proportionalität zwischen Handgröße und Körpergröße sein kann, sondern nur eine Korrelation.
Zuerst, wie kommt so eine Formel zustande? Eine Statistik legt den Verdacht nahe, dass mehrere Größen einen Zusammenhang haben könnten. Mit Regressionsanalyse versucht man eine Formel herzuleiten, die einem erlaubt, mit einer entsprechenden Trefferquote verlässliche Aussagen zu treffen. In unserem Fall, es gibt einen verlässlichen Zusammenhang zwischen Handgröße, Körpergröße und Alter.
Bloß in dieser Form bringt uns die Formel nicht weiter.
Ich habe diese Formel umgeformt
Handgröße = (Körpergröße – 80,400 + 0,195 * Alter – 6,383 * (Geschlecht: Frau = 0, Mann =1) )/ 5,122
und damit gerechnet.
Damit haben Kinder mit zwei Jahren Hände, die kleiner als ein Zentimeter sind.
Die untersuchte Population waren Erwachsene über 20 Jahre, die nicht mehr wachsen.
0,195 × Alter dürfte ein Ausgleich für das Schrumpfen mit zunehmenden Alter sein. In der Studie wird das so nicht erklärt. Die beschreiben ein paar Eckdaten der Regressionsanalyse und dann steht plötzlich die Formel da.
Deswegen habe ich beim Alter 20 eingesetzt.
Und erhielt je nach Geschlecht folgende Formel
Handgröße=(Körperhöhe – 76,9)/5,122
Handgröße = (Körperhöhe – 70,117)/5,122
Bloß hier kommen Handgrößen bei den Zweijährigen zwischen knapp einem Zentimeter und vier Zentimeter. Was auch nicht der Realität entspricht.
Meine Idee, die Zahlen 76,9 und 70,117 sind die Teile der Körpergröße, die keinen Einfluss auf die Handgröße haben. Nur ein Teil des Körpers zählt. Aber diese Zahlen gelten für Erwachsene, die nicht mehr wachsen. Also, warum diesen Anteil nicht entsprechend der Größe der Kinder umrechnen. In diesen Größencharts gibt es immer eine Mediangruppe. Das ist die Gruppe, in die die meisten Leute fallen. Die weitere Idee, ich nehme die Größe der ältesten Gruppe in der Mediangruppe und verrechne die mit der Größe der jüngeren Gruppen.
Also:
Handgröße = (Körperhöhe – Körperhöhe/Mediangröße*76,9)/5,122
Handgröße = (Körperhöhe – Körperhöhe/Mediangröße*70,117)/5,122
Alternativ habe ich noch versucht,
Handgröße = (Körperhöhe – Körperhöhe/Maximale_Größe_in_Größengruppe*76,9)/5,122
Handgröße = (Körperhöhe – Körperhöhe/Maximale_Größe_in_Größengruppe*70,117)/5,122
Sind die jetzt berechneten Handgrößen realistisch? Ich vermute ja. Denn beim Verhältnis Körpergröße zu Handgröße bewegen sich die Werte zwischen 8 und 10. Das ist auch die Größenspanne, die in einer der Studien, für das Verhältnis von Handgröße und Körpergröße beschrieben wird.
Man kann diese Formeln noch weiter umformen.
Handgröße = Körperhöhe (1 – 1/Mediangröße*76,9)/5,122
Handgröße = Körperhöhe (1 – 1/Mediangröße*70,117)/5,122
Handgröße = Körperhöhe (1 – 1/Maximale_Größe_in_Größengruppe*76,9)/5,122
Handgröße = Körperhöhe (1 – 1/Maximale_Größe_in_Größengruppe*70,117)/5,122
Demnach bliebe die Handgröße in der Wachstumsphase direkt proportional zur Körpergröße.
Warum verwende ich den Konjunktiv?
Die Ausgangsformel deutet an, dass bei kleineren Körper die Hände im Verhältnis zur Körpergröße kleiner sind. Wenn man von einem kleineren Körper zu einem großen Körper wächst, soll das also nicht gelten?
Ein Grund für das Phänomen könnte sein, dass diese Formel trotz dieser impliziten Aussage, den Test ihrer Eignung bestanden hat, obwohl diese implizite Aussage in Realität nicht zutrifft. Es kann aber auch sein, dass die Formel genau die Realität kleine Körper haben im Verhältnis kleinere Hände beschreibt.
Das ist aber nicht Thema in den Studien, sondern es wird der mathematische Weg beschrieben. Entweder die Mathematik geht auf oder nicht. Es wird nicht darüber reflektiert, was für Interpretationen diese Formeln zulassen und ob diese Interpretationen sinnvoll sind. Es soll nur bewiesen werden, dass Daten korrelieren. Über Kausalitäten und Interpretationen macht man sich dann in anderen Studien Gedanken.
Also machen wir eine Fallunterscheidung.
Gehen wir von einer direkten Proportionalität der Handgröße zur Körpergröße aus, dann gilt das auch für die Dehnung zwischen den Fingern.
Gehe ich von dieser Überlegung aus, dann kann man mit diesen Wachstumsstatistiken sagen,
- was für eine Mensur der*i Erstklässlerin als Erwachsener braucht.
- wann die nächste Gitarre gekauft werden muss.
Sollte doch gelten, dass die Hände schneller oder anders wachsen als der Körper, dann würde ich immer noch eine Prognose aufgrund der Statistik wagen, wann braucht es die nächste Gitarre und diese leicht nach unten korrigieren.
Die Langfristprognose sollte man aber dann mit Vorsicht genießen.
Mängel im System
Dehnfähigkeitszugewinn
Diese Prognosen können eigentlich nur für Menschen funktionieren, die schon eine Zeit lang Gitarre spielen. Denn man gewinnt durch das Spielen ein gewisses Maß an Dehnfähigkeit. Das sind bei manchen Schülern fünf Millimeter. Bei anderen Schülern aber nur ein bis zwei Millimeter. Bei Erwachsenen sind diese Differenzen besonders ausgeprägt. Das Problem ist, wie stellt man über eine Hand, die man nicht kennt, eine Prognose an, wie viel Dehnfähigkeit wird sie dazu gewinnen? Das geht vermutlich nicht einmal, wenn man die Hand kennt.
Aber auch hier haben wir jetzt Zahlen, die bei der Diskussion helfen. Mein Schüler vom Anfang kann auf einer Normalmensur so gerade am dritten Bund mit 1 und 3 greifen. Das bedeutet für seine 1,90 für ihn passt eine 58 cm Mensur. Als Klavierbauer gefällt ihm ja schon die Idee mit 63 cm nicht. Er ist voll Optimismus, er kann die fehlenden 1,1 cm noch erkämpfen. Aber wenn man bedenkt, das sind ca. 4 Jahre Körperwachstum oder 20 Prozent seiner momentanen Dehnfähigkeit, dann kann ich ihn doch noch von einer 63-er überzeugen.
Fazit und Disclaimer
Ich persönlich habe meine Schätzmethode auf stabilere Füße gestellt und fühle mich wohler, wenn die Frage kommt, wie oft müssen wir eine neue Gitarre kaufen. Vielleicht „streite“ ich mich auch noch mit der Patentante.
Aber ich habe zwei Situationen geschildert, wo Fachmeinung konträr gegen Fachmeinung stehen. Damit fühle ich mich wesentlich wohler, weil ich den Leuten quasi vorrechnen kann, wie die Sache sein dürfte.
Momentan habe ich auch das Problem, dass für eine Vierzehnjährige die Endgitarre angeschafft werden soll. Ich mag diese Endbestimmung der Endgröße der Gitarre bei Mädchen nicht, weil mir nie klar war, wie finde ich heraus Untermensur oder Normalmensur.
Ich habe mir die Größe der Mutter angehört, dachte an meine Arzteltern, die uns Kinder bei der Partnerwahl empfahlen: „Schau dir die/den Mutter/Vater an und überlege es dir noch einmal.“ Ich entschied 65. Mit der Methode gehe ich auf 63 cm. (Leider muss ich der Schülerin mitteilen, dass sie kleiner bleiben wird als ihre Mutter.)
Ich möchte darauf hinweisen, dass die Methode nur ein Modell ist, was sich in der Realität beweisen muss. Mir als einzelnem Lehrer ist es unmöglich so viel Datenmaterial durch die begrenzte Schüler*Innenschar zu kreieren, sodass man die Methode wasserfest beweisen ist.
Aber ich hoffe Zahlen und Größenordnung geschaffen zu haben, sodass eine Diskussion nicht mehr Erfahrung gegen Erfahrung, oder sogar Meinung gegen Meinung ist. Weiter kann man auch eher Eltern beruhigen, die Sorge vor zu häufigem Gitarrenkauf haben.
Ob diese Herangehensweise gerade an der Dehnfähigkeit des ersten und dritten Fingers aufgehängt werden muss? Weiter ist die Forderung sinnvoll, dass die zwei Finger das c und d einigermaßen mühelos greifen sollen, oder wäre cis dis nicht sinnvoller?
Man kann auch andere Fingerkombinationen und Bundabstände verwenden. Die Abstände der Bünde berechnet man durch die Formel:
Bundabstand = Mensur/ (1/2^(tiefer Bund/12) – Mensur/ (1/2^(hoher Bund/12)
Aus der Dehnung berechnet man die geeignete Mensur mit dieser Formel:
Mensur = Dehnung/(1/2^(tiefer Bund/12)-1/2^(hoher Bund/12))
Dies ist die Formel, wenn die Dehnung nicht an einer Gitarre gemessen wurde. Es geht unter Umständen einfacher.
Wenn man die Dehnung an einer Gitarre misst, und feststellt, stellt fest, dass Kind greift am x-ten Bund am besten, dann müsste bei der optimal geeigneten Gitarre, der Sattel am x-1-ten Bund sein. Das bedeutet die Mensur der Zielgitarre berechnet sich:
Mensur_Zielgitarre = Mensur_Messgitarre * 2^((x-1)/12)
Letztlich bleibt, dass die Methode, ich schaue mir die Greifhand am Griffbrett an und sagen dann was, vielleicht etwas mehr Zuverlässigkeit gewinnt.
Der Beitrag wurde am Freitag, den 7. Oktober 2022 um 08:08 Uhr veröffentlicht von Stephan Zitzmann und wurde unter den Kategorien: Gitarre lernen, Gitarrenunterricht, Instrumente, Kinder, praktisch abgelegt. | Es gibt keinen Kommentar .

